The Fourier transform is quite often used to solve various kinds of PDEs involving a single spatial dimension, such as in the case of audio signal processing. However, the Fourier transform (and other related transforms) can in fact be expanded to an arbitrary number of dimensions for all kinds of interesting applications.
The Goal
The goal of this post is to expand the concept of the Fourier transform to two dimensions and then use it to solve the classic wave and heat equations.
The Toolset
There are many kinds of transforms we could use to achieve our goal, but I’ve chosen to use a transform known as the Fourier-Bessel transform (or Hankel transform), which I will denote $\mathscr{B}$. In essence, the Fourier-Bessel transform is a technique of integrating the product of an arbitrary radial function $u(r)$ and an integral kernel, in this case the zero-order Bessel function of the first kind $J_0(\lambda r)$:
\[\mathscr{B}(u(r)) = \int_{0}^{\infty} u(r) J_0(\lambda r) r \,dr = u(\lambda)\]
This style of transform is particularly suited for radially symmetric functions. It enables us to reorganize the information of $u(r)$ in terms of Bessel functions involving a “frequency” variable $\lambda$. Converting backwards from $\lambda$ to $r$ is possible with the inverse Fourier-Bessel transform:
\[\mathscr{B}^{-1}(u(\lambda)) = \int_{0}^{\infty} u(\lambda) J_0(\lambda r) \lambda \,d\lambda = u(r)\]
We can use the Fourier-Bessel transform to solve both the wave equation and the heat equation by converting them from difficult PDEs into easy ODEs, and the approach is similar to that used for the simpler one-dimensional Fourier transforms.
The Key to Solving Our Equations
The key to solving these PDEs is to take advantage of a crucial property of the Fourier-Bessel transform, namely the relationship between the Fourier-Bessel transform of a function, $\mathscr{B}(u(r))$, and the Fourier-Bessel transform of the Laplacian of the function, $\mathscr{B}(\Delta u(r))$. The Laplacian for two-dimensional polar coordinates is defined as:
\[\Delta u(r,\theta) = u_{rr} + \frac{1}{r}u_r + \frac{1}{r^2}u_{\theta\theta}\]
Now, since our function $u(r)$ is radially symmetric and thus doesn’t depend on $\theta$, the equation above simplifies to:
\[\Delta u(r) = u_{rr} + \frac{1}{r}u_r\]
(Remember I said the Fourier-Bessel transform is particularly suited for radially symmetric functions? This is why.)
Then, with a little bit of effort, the relationship between $\mathscr{B}(u(r))$ and $\mathscr{B}(\Delta u(r))$ can be shown:
\[\mathscr{B}(\Delta u(r)) = \int_{0}^{\infty} \left( u_{rr} + \frac{1}{r}u_r \right) J_0(\lambda r) r \,dr = -\lambda^2 \int_{0}^{\infty} u(r) J_0(\lambda r) r \,dr = -\lambda^2 \mathscr{B}(u(r))\]
The fact that $\mathscr{B}(u(r))$ and $\mathscr{B}(\Delta u(r))$ are proportional via the coefficient $-\lambda^2$ is the property that gives us the means of converting our PDEs into ODEs, and in turn solving them more easily.
The Wave Equation Solution
The following conditions collectively define the wave equation we are trying to solve. Note that $u$ now has an added time component $t$.
| The Wave Equation | $u_{tt} = \Delta u$ |
|---|---|
| Initial Condition | $u(r,0) = e^{-r^2/2}$ |
| Boundary Condition | $u(\infty,t) = 0$ |
Our strategy is to apply the Fourier-Bessel transform to each of these three conditions. I’ve chosen a Gaussian initial condition for the sake of convenience, since then it becomes trivial to transform: $\mathscr{B}(e^{-r^2/2}) = e^{-\lambda^2/2}$. Applying the transform to all three conditions, we get:
| $u_{tt} = \Delta u$ | $\Rightarrow$ | $u_{tt} = -\lambda^2 u(\lambda,t)$ |
|---|---|---|
| $u(r,0) = e^{-r^2/2}$ | $\Rightarrow$ | $u(\lambda,0) = e^{-\lambda^2/2}$ |
| $u(\infty,t) = 0$ | $\Rightarrow$ | $u(\infty,t) = 0$ |
On the left is the original wave PDE, and on the right is a much easier ODE. It’s not hard to show that these transformed conditions yield the following solution for $u(\lambda,t)$:
\[u(\lambda,t) = e^{-\lambda^2/2}\cos{\lambda t}\]
The presence of the cosine indicates that this function will oscillate with time—precisely how a wave should behave. With this solution for $u(\lambda,t)$, we can convert back to our original function $u(r,t)$ by taking an inverse Fourier-Bessel transform:
\[u(r,t) = \mathscr{B}^{-1}(u(\lambda,t)) = \int_{0}^{\infty} e^{-\lambda^2/2} \cos{\lambda t} J_0(\lambda r) \lambda \,d\lambda\]
Instead of solving this integral analytically, I used Wolfram Mathematica to calculate it numerically and plot the solution as a pretty spectacular animation:
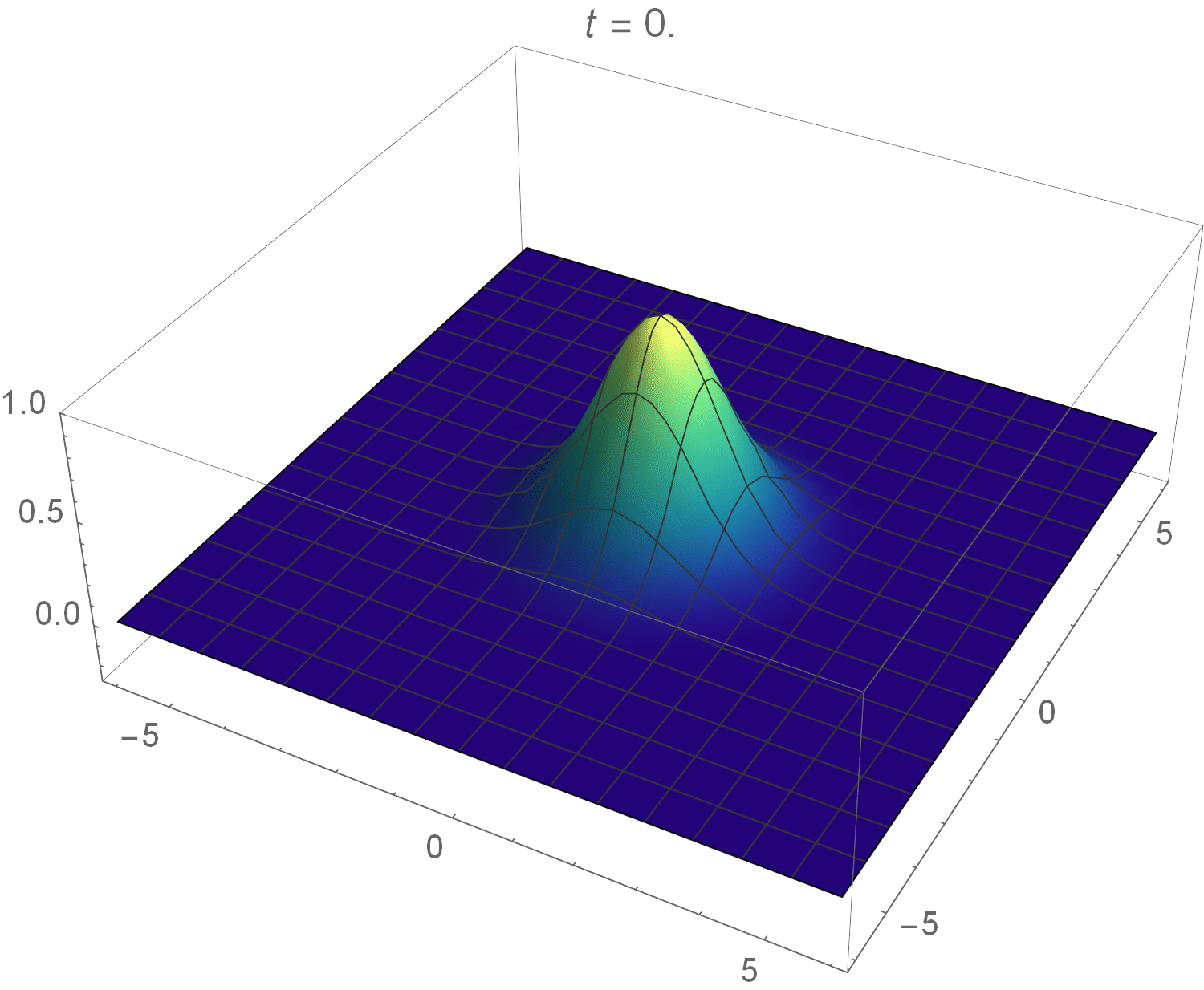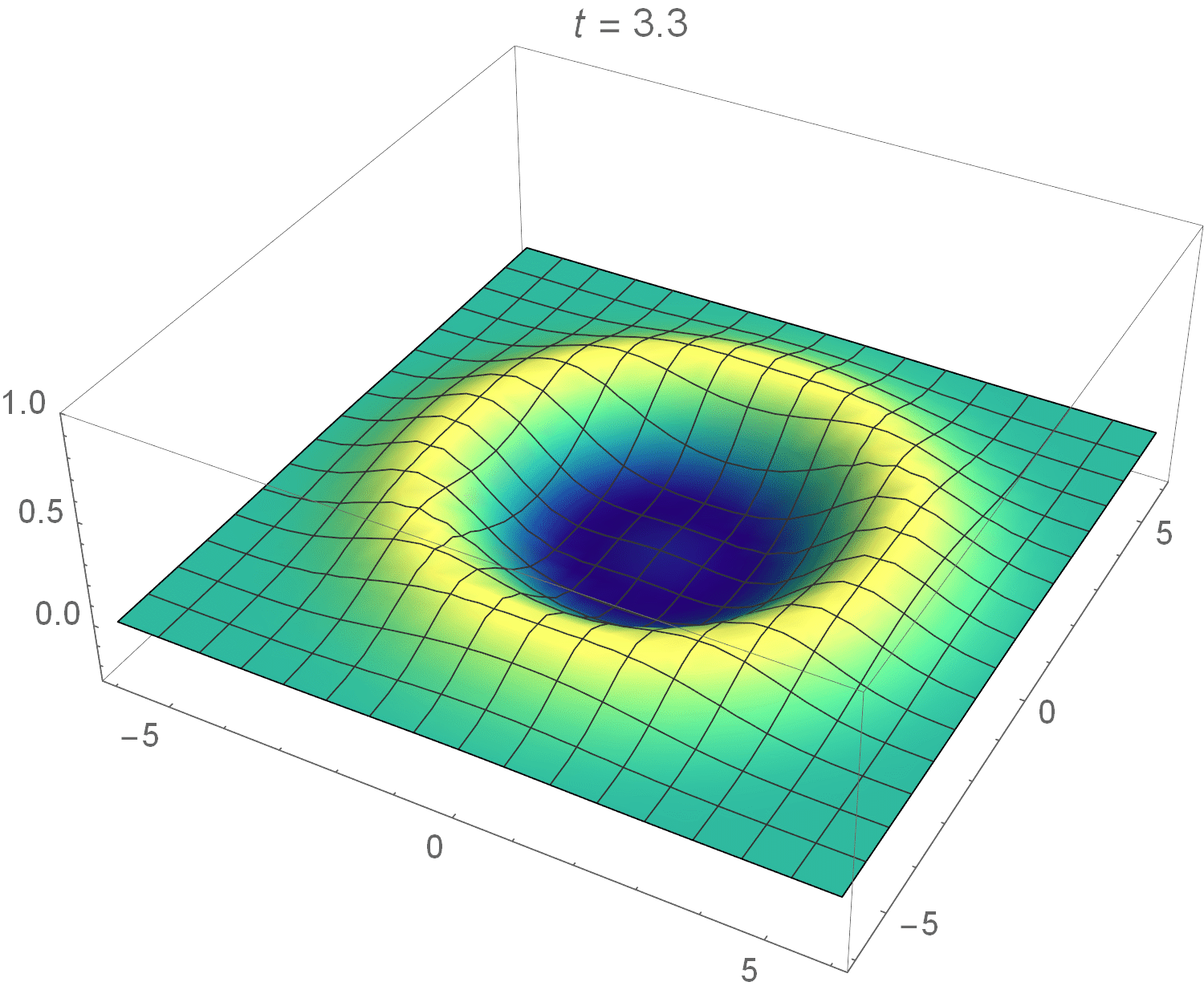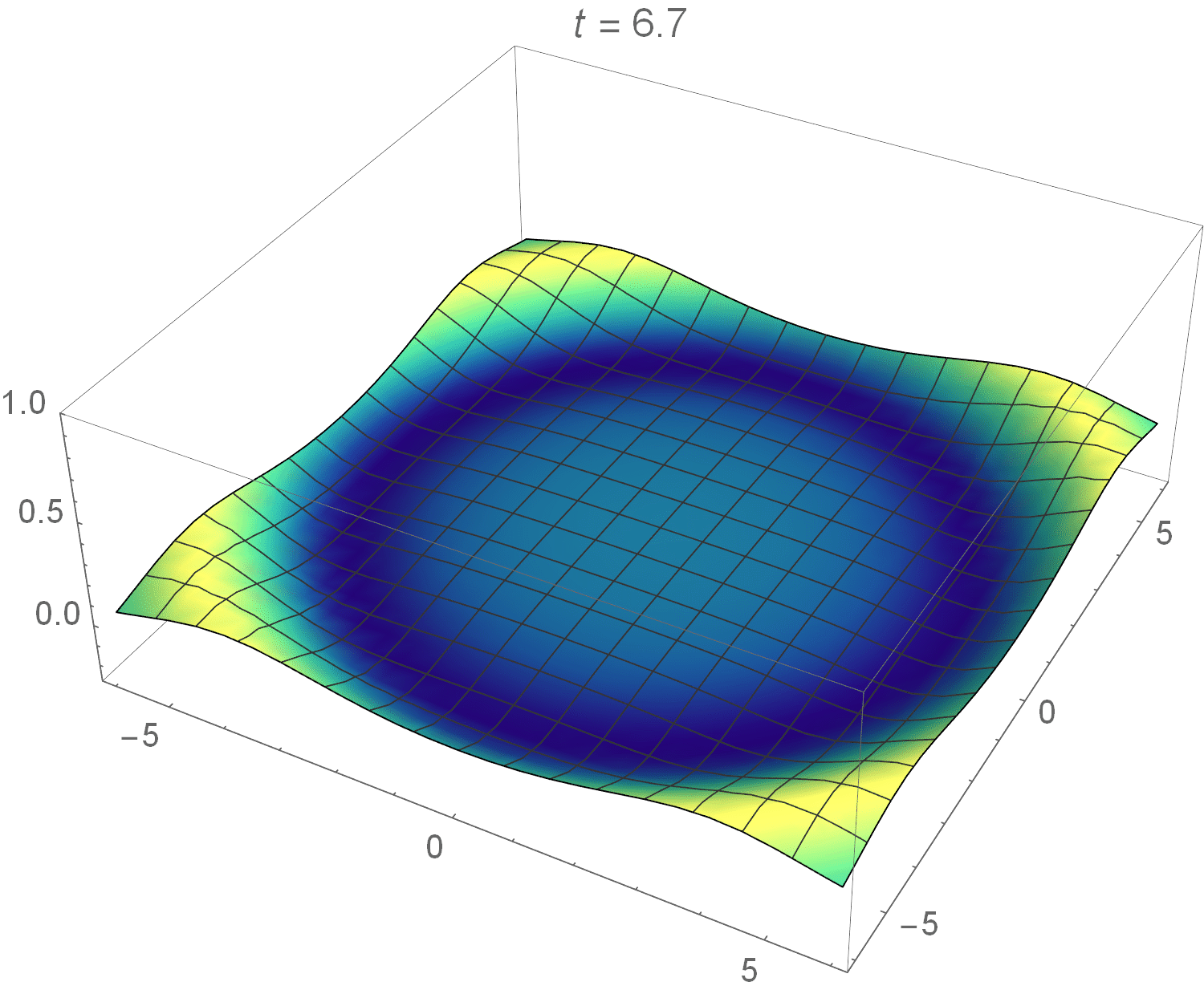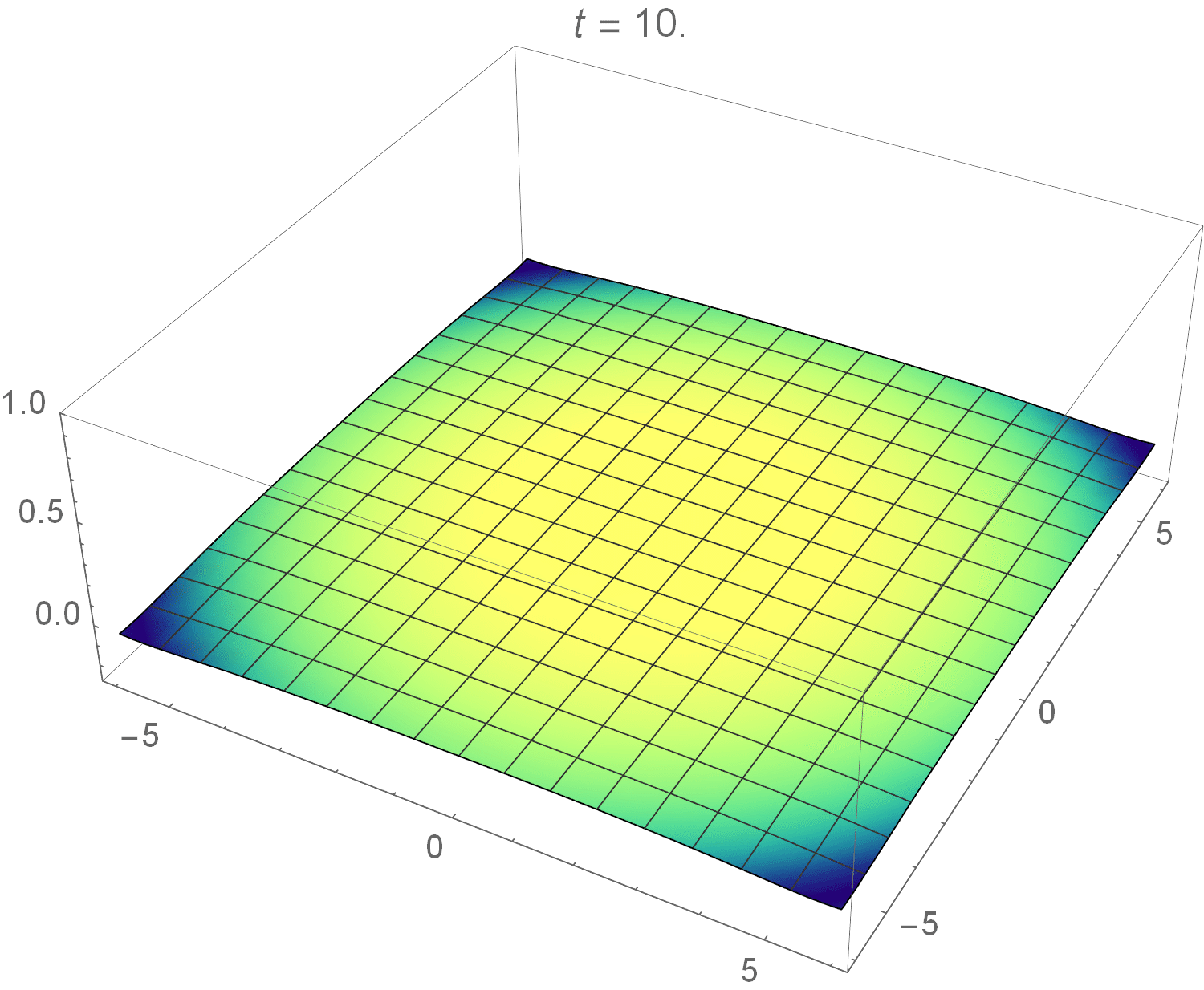
It looks exactly like it what it should: a radially symmetric wave!
The Heat Equation Solution
The heat equation setup is very similar to that of the wave equation, except with $u_t$ replacing $u_{tt}$.
| The Heat Equation | $u_t = \Delta u$ |
|---|---|
| Initial Condition | $u(r,0) = e^{-r^2/2}$ |
| Boundary Condition | $u(\infty,t) = 0$ |
Following the same strategy as before, we transform all three conditions to get:
| $u_t = \Delta u$ | $\Rightarrow$ | $u_t = -\lambda^2 u(\lambda,t)$ |
|---|---|---|
| $u(r,0) = e^{-r^2/2}$ | $\Rightarrow$ | $u(\lambda,0) = e^{-\lambda^2/2}$ |
| $u(\infty,t) = 0$ | $\Rightarrow$ | $u(\infty,t) = 0$ |
The solution to this is similarly straightforward to derive, and it ends up looking somewhat different than the one for the wave equation:
\[u(\lambda,t) = e^{-\lambda^2/2} e^{-\lambda^2 t}\]
Clearly this function will dissipate with time rather than oscillate, just like heat does in real life. Taking the inverse Fourier-Bessel transform, the final solution becomes:
\[u(r,t) = \mathscr{B}^{-1}(u(\lambda,t)) = \int_{0}^{\infty} e^{-\lambda^2/2} e^{-\lambda^2 t} J_0(\lambda r) \lambda \,d\lambda\]
I animated this one in Mathematica as well. Here’s the result:
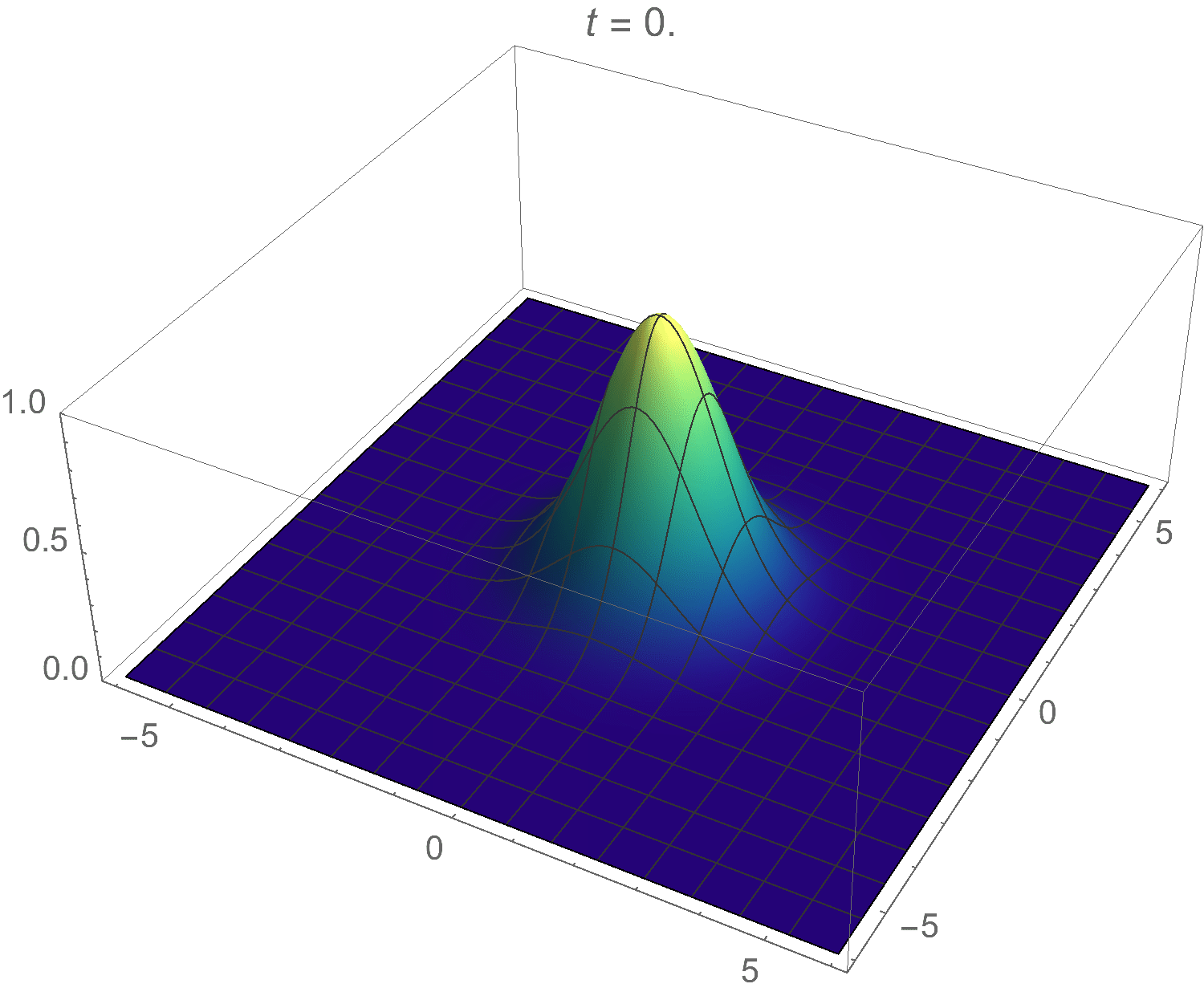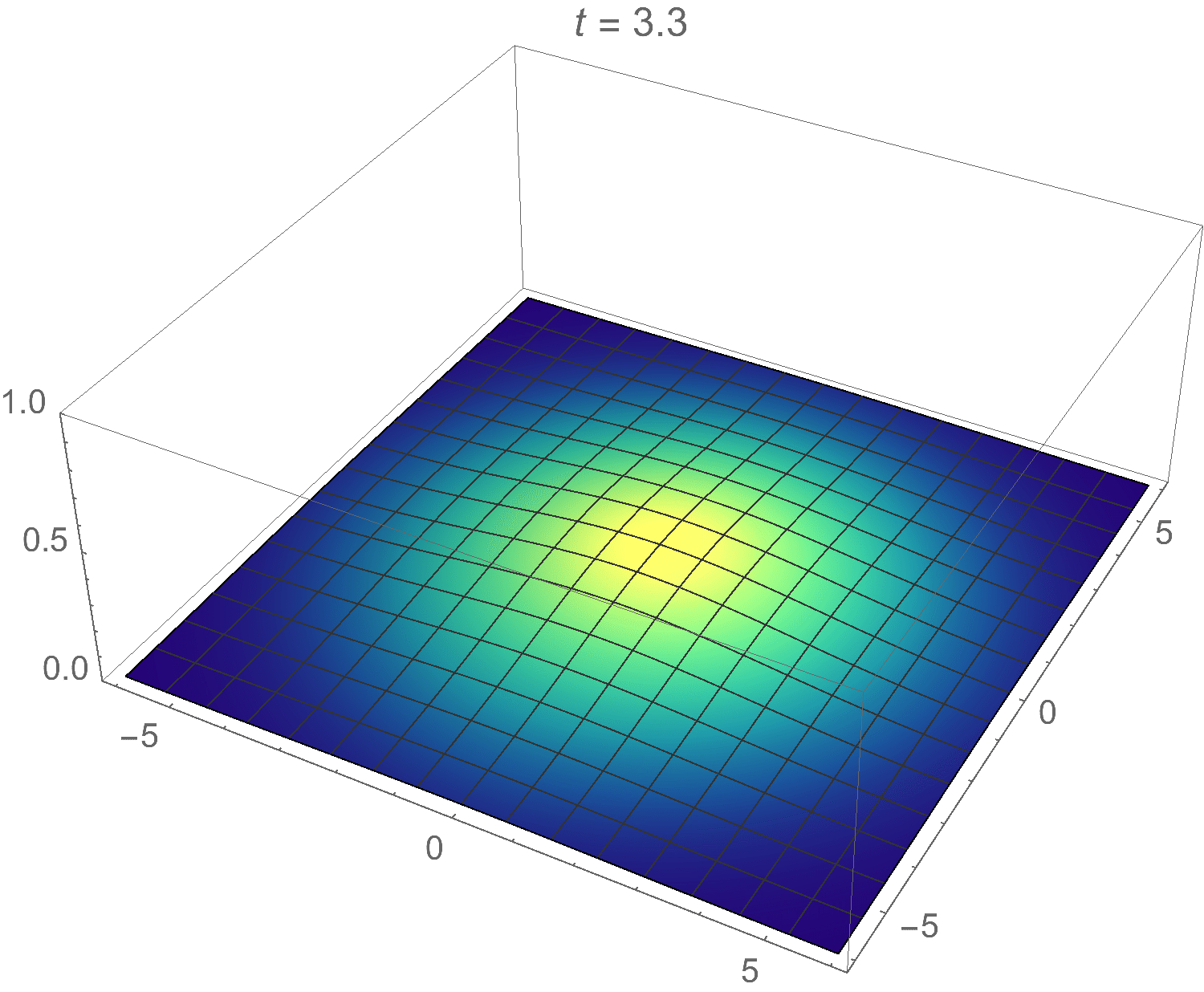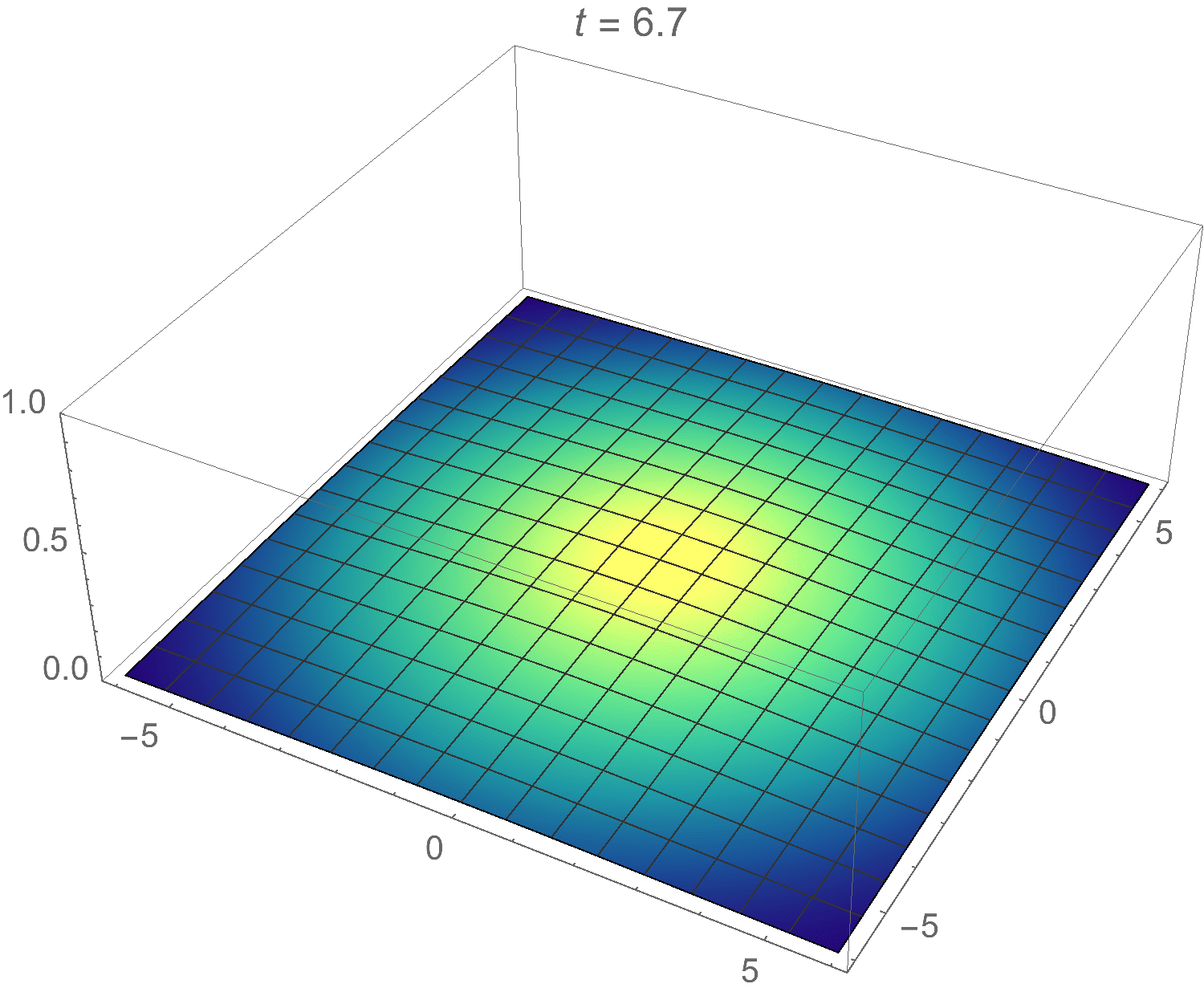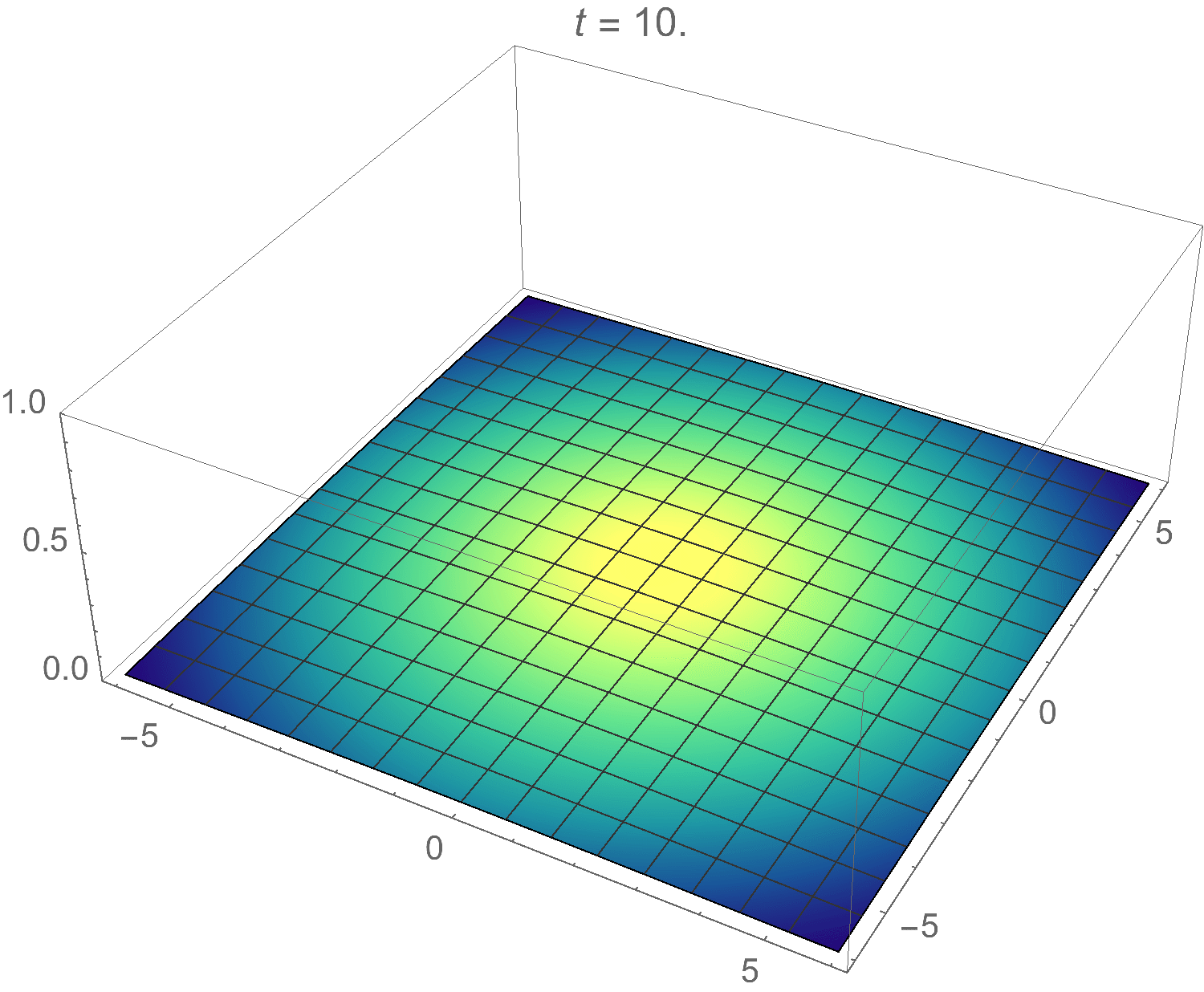
Pretty cool! (Or should I say hot?)
How I Generated the Animations
I created animations of my solutions using Wolfram Mathematica. I already had some experience making 3D plots in Mathematica, but I had to jump through several hoops in order to make the computation times manageable! Since Mathematica performs symbolic calculations by default, I had to add a few extra lines of code to tell it to stick to purely numerical calculations, which can be done much faster. Because of this numerical approach, I had to take some shortcuts, such as setting the bounds of integration in my solutions from 0 to 10 instead of 0 to $\infty$. This drastically reduced computation time, and I figured that it would be close enough since it gets cut off at a factor of $e^{-100}$, which seems close enough to 0.
Also, even though I found my solutions as functions of a radial coordinate $r$, I plotted them as functions of Cartesian coordinates $x$ and $y$. Essentially, I just plugged in $r = \sqrt{x^2 + y^2}$ for the spatial coordinate. This was so that I could more easily prevent the vertical axis from re-scaling automatically, which isn’t so simple when plotting in polar coordinates in Mathematica.